It’s confusing to to me when I went through 2 different terminologies LinearRegression in Scikit-learn and polyfit (polynomial least squares) in Numpy libraries. What are differences between these and how we can use the libraries differently? Both seem to be living in the same world “least squares” thing and they are capable for finding a linear model with coefficients and intercept by minimizing the residual sum of squares.
It’s said that least squares problems fall into two categories: linear or ordinary least squares and non-linear according to Wikipedia. The linear least-squares problem occurs in statistical regression analysis and the polynomial least squares also fall into regression analysis. Polinomial regression technique models the relationship between the independent variable x and the dependent variable y as an nth polynomial in x. Are these the same?
I had no idea what sort of math and implmentation are behind both libraries Scikit-learn LinearRegression and Numpy polyfit, however they looked quite similar and the implementations could be the same as the functions return quite similar coefficients and intercepts in the following expriment. In this blog, I tested both Scikit-learn.LinearRegression and Numpy.polyfit for fitting curves.
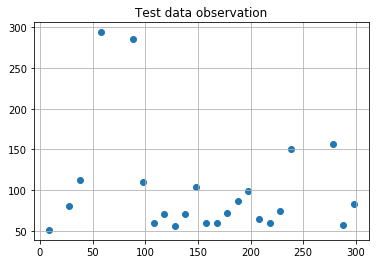
For this experiment, I used this simple arrays for data set. I also defined a function returning standard errors. We will use this function for polyfit models to compute the standard errors.
Numpy.polyfit
It simply explains Numpy.polyfit does least squares polynomial fit. It returns a vector of coefficients and an intercept in numpy.ndarray. The highest power comes first in that array and the last item is the intercept of the model. This function uses least squares and the solution is to minimize the squared errors in the given polynomial.

It states clearly polynomial regression leverages least squares for computation and it can model the expected dependent variables y as an nth degree polynomial, yielding the general polynomial regression model. A maze in first place was that linear function unveils non-linear relationship between the independent variable x and the dependent variable y.
Why is it called “linear” then? The word “linear” means the regression function is linear to estimate the unknown parameters. In Wikipedia, the computational and inference part of polynomial regresion rely on multiple linear regression by treating x, x2, … as being distinct independent variables in a model. Let’s take a look how we can run a code in Numpy.polyfit.
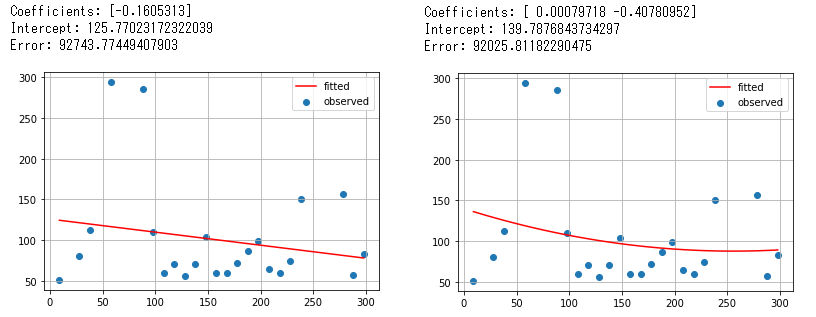

The coefficients must have been estimated using ordinary least squares estimation. Let’s move to Scikit-learn.LinearRegression.
Scikit-learn.LinearRegression
We looked through that polynomial regression was use of multiple linear regression. Scikit-learn LinearRegression uses ordinary least squares to compute coefficients and intercept in a linear function by minimizing the sum of the squared residuals. (Linear Regression in general covers more broader concept). Here’s the official documentation and I don’t find much differences between polynimial regression and linear regression at a high level.
1 obvious difference is that LinearRegression library treats simple linear regression and ordinary least squares, not assusme polynomial at a glance. But there is an extension we can add polynomial features into LinearRegression, which could bring the same computation as Numpy.polyfit does. Once you fit a model using LinearRegression library in Scikit-learn, coef_ and intercept_ will be callable to get coefficients and intercept from the fitted model.
Here’s the code to fit the models of 1 and 2 degree polynomial (only 2 degree can be called polynomial in this code). Afterwards I repeated the same patterns for 3 and 4 degree.
Next, I defined the drawing function and gave the parameters of 1 to 4 degree polynomial models we’ve just generated above. The graphs look jerky a little compared to Numpy.polyfit ones. I don’t know why.
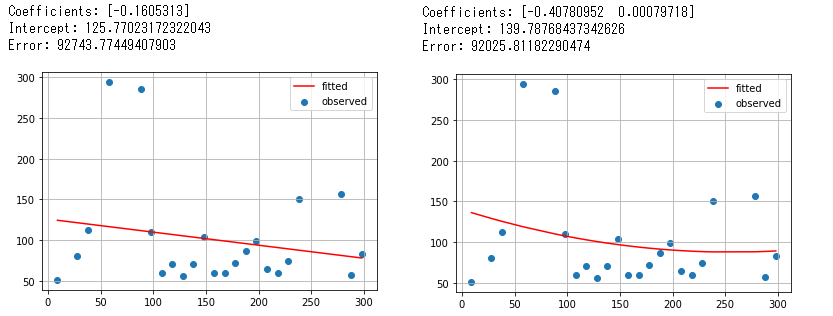
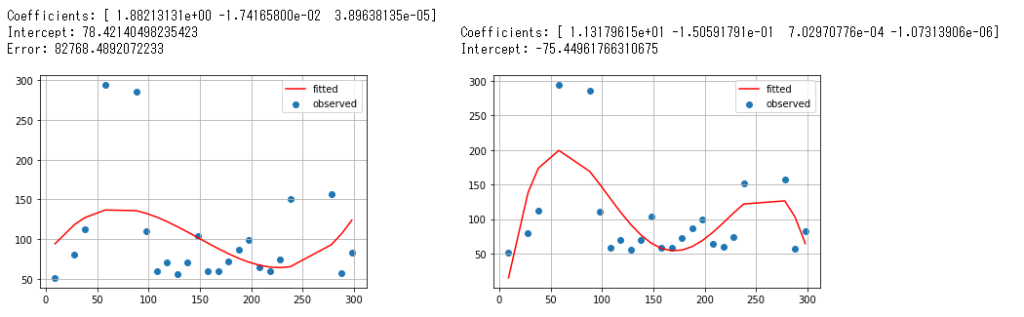
coef_ returns lowest power first opposite to polyfit’s result. Look at those coefficients and intercepts, errors. There are slightly differences in after smaller decimal places but we can say those are the same roughly. At least they seem to be using the same math formula (but not sure the implementation in Python behind the libraries).
To wrap up, polynomial regression leverages ordinary least squares in computation and from this perspective, it is just a case of multiple linear regressions, while polynomial is an application of linear regression and in Scikit-learn.LinearRegression there is an extension PolynomialFeatures and it can be solved with the same techniques.
finance_python/Scikit-learn LinearRegression vs Numpy Polyfit.ipynb
- Polynomial regression leverages ordinary least squares to estimate the unknown paramters in a linear function
- An interpretation of a fitted polynomial regression model might require somewhat different perspective (read here Interpretation)
- Numpy.polyfit and Scikit-learn.LinearRegression with PolynomialFeatures might be used interchangeably because those return the same coefficients and intercepts